一个简单的物理引擎
之前物理课的时候看到了PPT上一张分子热运动的图,觉得很有趣,于是那个星期就做了个二维球体完全弹性碰撞的简单物理引擎。非常凑巧的是,刚好这个东西可以拿来做最后的物理大作业,也算是非常开心吧。
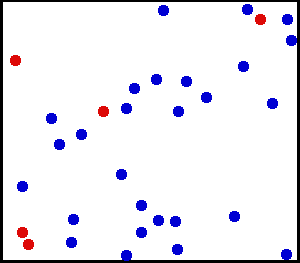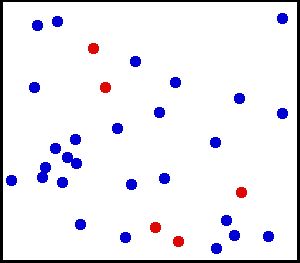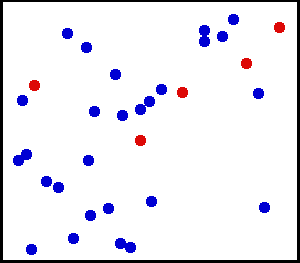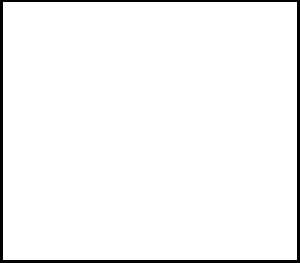
先放上这次物理大作业做的三个热学演示吧,其实核心代码是一样的,只不过根据不同演示的需要做了一定的修改:
写引擎之前我隐约知道,好像大部分的物理引擎都是在每一帧里面,让每个物体往前前进一点,然后当两个物体重叠之后再做碰撞的处理。但是我对这一套理论十分的不了解,而且总是觉得这么做十分的麻烦,又怕当碰撞十分复杂的时候(比如接连有好多个物体碰撞)会出问题,所以我决定按照另外一个十分显然的思路来写引擎。
引擎
因为我只要模拟球和球以及球和墙之间的碰撞,所以我实际上只做了一种物体,就是二维的球。每一个球的位置向量是关于时间的函数:
\[ \mathbf{r}(t) = \mathbf{p} + \mathbf{v}*t \]
因此很容易可以通过解方程求得两个球碰撞的时间
\[ \left | \mathbf{r_1}(t)-\mathbf{r_2}(t) \right |=2R \]
于是引擎在运行的时候实际上就是记下下次碰撞事件的时间,如果当前时间小于下一次碰撞事件的时间,那么就不管它,只管根据函数算出每个点的位置,然后画图就好了。
而当当前时间超过了下一次碰撞事件的时间的时候,就要先重新计算碰撞之后物体新的函数\(\mathbf{r’}(t)\),然后再次计算下次碰撞的时间,如果依然在当前时间之前,那么就继续更新,直到下一次碰撞事件的时间大于当前的时间。
完全弹性碰撞的话,从维基百科可以找到下面的公式:
\[\begin{matrix} \mathbf{v_1'}& = & \mathbf{v_1}-\frac{2m_2}{m_1+m_2} \frac{\left \langle \mathbf{v_1}-\mathbf{v_2},\mathbf{x_1}-\mathbf{x_2} \right \rangle}{\left \| \mathbf{x_1}-\mathbf{x_2} \right \|^2}(\mathbf{x_1}-\mathbf{x_2})\\ \mathbf{v_2'}& = & \mathbf{v_2}-\frac{2m_1}{m_1+m_2} \frac{\left \langle \mathbf{v_1}-\mathbf{v_2},\mathbf{x_1}-\mathbf{x_2} \right \rangle}{\left \| \mathbf{x_2}-\mathbf{x_1} \right \|^2}(\mathbf{x_2}-\mathbf{x_1}) \end{matrix}\]这样看来,引擎还是很简单的嘛。
维护碰撞事件
可以看出来,引擎需要解决的一个核心问题是碰撞事件的维护。
\(O(N^{2})\)
最普通的方法可以当一次碰撞发生之后,计算物体两两之间的碰撞事件,取然后取最近的一次碰撞事件作为下一次的碰撞时间。我一开始就是这么做的,复杂度是 \(O(N^2)\) ,非常不乐观,基本上只能支撑400个点的流畅动画。
\(O(NK)\)
之后我想了一个办法来优化。实际上,碰撞发生之后,并不是每个点的下一次碰撞事件都会变,因为这一次碰撞的发生,只会改变这次碰撞的两个物体的函数。如果我们记下了每个点的下一次碰撞事件,那么一次碰撞发生后,只有下一次碰撞事件是和当前发生碰撞的物体发生的那些物体,它们的下一次碰撞事件会失效,需要重新计算。
因此,我们找出下一次碰撞事件是和当前碰撞物体碰撞的物体,假设有 \(K\) 个,那么,重新计算这 \(K\) 个点的下一次碰撞事件就好了(当然啦,当前碰撞的这两个也得算)。
这样做的复杂度是 \(O(NK)\) 的。虽然当 \(K=O(N)\) 时,这个算法还是 \(O(N^2)\) 的,但是我统计了一下, \(K\approx 0.01N\),因此实际表现还是非常好的。
\(O(N\log N)\)
沿着上面的思路,很容易想到,如果维护每个点的碰撞事件队列的话,那么一次碰撞发生之后只需要重新计算发生碰撞的两个物体的碰撞队列即可,碰撞事件的重新计算量由 \(O(NK)\) 减少至 \(O(N)\)
具体来说就是这样,当x和y碰撞发生时:
- 将所有点的碰撞事件队列中,与
x和y碰撞的事件发生的时间,标记成 \(+\infty \) - 重新计算
x和y的整个碰撞事件队列 - 扫一遍所有点的碰撞事件队列,找出下一次碰撞时间最近的碰撞事件,作为下一次碰撞事件
那么这个碰撞队列怎么实现呢?自然是堆啦,一个简单的堆就能实现这个操作了。
经统计,用这个方法,比上面那个方法,在相同条件下,少计算了65%的碰撞事件。
更好的方法?
不幸的消息是,虽然上面第三个方法看起来十分厉害,但是实际上跑起来比起第二个方法,卡顿明显,主要原因可能是当点数较少,比如1000个点的时候,堆带来的额外时间比减少的碰撞事件计算更多。
我感觉应该还是有一些更精妙的方法的,比如对屏幕分块,然后下一次碰撞不会发生在离的很远的块中,这样的话只需要在局部重新计算即可。
然而具体的方法确实我是不知道的,或许这个留个坑以后来填?
可视化
我目前唯一会的可视化方法就是 HTML5 Canvas,我觉得配合起 javascript 还是蛮方便的。一开始是直接对 canvas 做操作,后来发现了一个 pixi.js 专门用作对画布的操纵,支持 WebGL ,还提供了 canvas 作为备用,并且还挺好操作的,因此后来就改用了这个库。不过很可惜,目前瓶颈还是在计算碰撞事件上,因此性能的提高并不明显。
统计图的话,还是老样子用 c3.js,用起来还是很开心的。